segi banyak adalah

Segi banyak adalah suatu bentuk geometri dua dimensi yang dibatasi oleh sejumlah ruas garis yang saling terhubung. Ruas garis-garis ini disebut sisi, dan titik-titik pertemuan antara dua sisi disebut titik sudut. Jumlah sisi dan titik sudut pada segi banyak selalu sama. Segi banyak merupakan konsep dasar dalam geometri dan memiliki banyak aplikasi dalam kehidupan sehari-hari, mulai dari desain bangunan hingga pembuatan pola pakaian. Pemahaman yang mendalam tentang segi banyak sangat penting, baik untuk studi matematika lanjutan maupun aplikasi praktis dalam berbagai profesi.

Artikel ini akan membahas secara mendalam tentang segi banyak, mulai dari definisi, jenis-jenis segi banyak, sifat-sifatnya, rumus-rumus yang berkaitan dengannya, hingga penerapannya dalam berbagai konteks. Kita akan menjelajahi dunia segi banyak dengan cara yang sistematis dan mudah dipahami, dilengkapi dengan contoh-contoh konkret dan ilustrasi yang membantu pemahaman Anda.

Sebelum kita menyelami lebih dalam, mari kita tinjau kembali beberapa definisi kunci. Seperti yang telah disebutkan, segi banyak adalah bangun datar tertutup yang dibatasi oleh garis lurus. Garis lurus tersebut membentuk sisi-sisi segi banyak, dan titik pertemuan antara dua sisi disebut sebagai titik sudut. Jumlah sisi dan titik sudut selalu sama pada suatu segi banyak. Konsep ini sederhana, namun menjadi dasar untuk memahami berbagai bentuk dan rumus geometri yang lebih kompleks.

Jenis-Jenis Segi Banyak

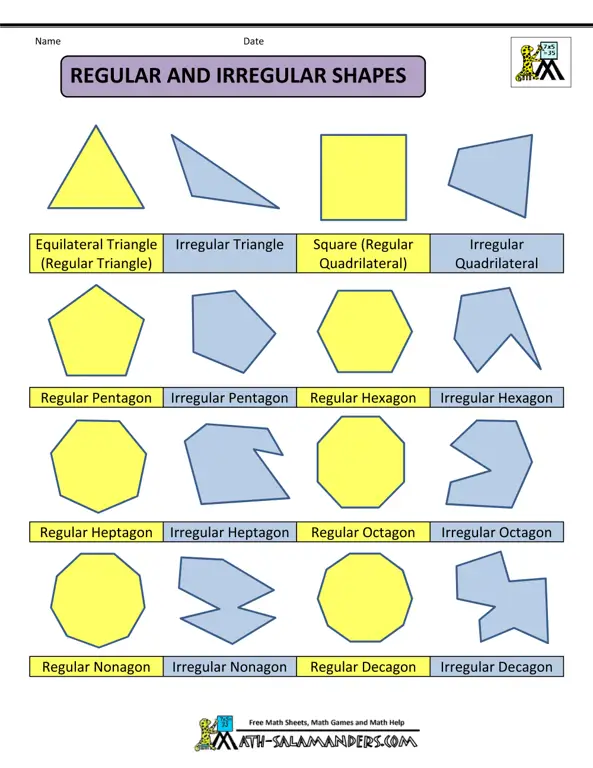
Segi banyak diklasifikasikan berdasarkan jumlah sisinya. Jumlah sisi menentukan nama dan sifat-sifat khusus dari segi banyak tersebut. Berikut adalah beberapa jenis segi banyak yang umum dipelajari, beserta penjelasan dan karakteristiknya:

• Segitiga (Trigon): Segi banyak dengan tiga sisi dan tiga sudut. Segitiga dapat diklasifikasikan lebih lanjut berdasarkan panjang sisi-sisinya (sama sisi, sama kaki, sembarang) dan besar sudut-sudutnya (lancip, siku-siku, tumpul). Segitiga merupakan dasar dari banyak konstruksi geometri lainnya.
• Segiempat (Quadrilateral): Segi banyak dengan empat sisi dan empat sudut. Segiempat memiliki beragam jenis, masing-masing dengan sifat dan rumus luas yang berbeda. Jenis-jenis segiempat yang umum antara lain: persegi, persegi panjang, belah ketupat, jajargenjang, trapesium, dan layang-layang. Mempelajari perbedaan dan sifat-sifat masing-masing segiempat sangat penting untuk memecahkan berbagai soal geometri.
• Segilima (Pentagon): Segi banyak dengan lima sisi dan lima sudut. Segilima dapat beraturan (semua sisi dan sudut sama) atau tidak beraturan. Segilima beraturan sering ditemukan dalam arsitektur dan desain.
• Segi Enam (Hexagon): Segi banyak dengan enam sisi dan enam sudut. Segi enam beraturan memiliki simetri yang unik dan sering digunakan dalam konstruksi sarang lebah dan struktur lainnya yang efisien.
• Segi Tujuh (Heptagon): Segi banyak dengan tujuh sisi dan tujuh sudut. Heptagon relatif jarang ditemukan dibandingkan segi banyak lainnya.
• Segi Delapan (Oktagon): Segi banyak dengan delapan sisi dan delapan sudut. Oktagon beraturan sering digunakan dalam desain bangunan dan simbol-simbol tertentu.
• Segi Sembilan (Nonagon): Segi banyak dengan sembilan sisi dan sembilan sudut.
• Segi Sepuluh (Dekagon): Segi banyak dengan sepuluh sisi dan sepuluh sudut.
• Segi Sebelas (Hendecagon): Segi banyak dengan sebelas sisi dan sebelas sudut.
• Segi Dua Belas (Dodecagon): Segi banyak dengan dua belas sisi dan dua belas sudut.

Dan masih banyak lagi jenis segi banyak dengan jumlah sisi yang lebih besar. Segi banyak dengan jumlah sisi yang sangat banyak sering disebut sebagai poligon. Semakin banyak sisi suatu poligon, bentuknya akan semakin mendekati lingkaran.

Sifat-Sifat Segi Banyak

Segi banyak memiliki berbagai sifat geometri yang menarik. Beberapa sifat penting yang perlu dipahami meliputi:

• Jumlah sudut dalam: Jumlah sudut dalam suatu segi banyak dengan n sisi dapat dihitung dengan rumus (n-2) x 180 derajat. Rumus ini berlaku untuk semua jenis segi banyak, baik beraturan maupun tidak beraturan.
• Jumlah sudut luar: Jumlah sudut luar suatu segi banyak selalu 360 derajat, berapapun jumlah sisinya. Sifat ini konsisten dan berguna dalam berbagai perhitungan geometri.
• Sisi-sisi dan sudut-sudut: Jumlah sisi dan sudut selalu sama pada suatu segi banyak. Ini merupakan sifat dasar yang mendefinisikan segi banyak.
• Kecekungan dan Kekembungan: Segi banyak dapat berupa cekung (memiliki sudut yang masuk ke dalam) atau cembung (semua sudutnya menonjol keluar). Segi banyak cekung memiliki sifat-sifat yang berbeda dengan segi banyak cembung.
• Segi Banyak Beraturan dan Tidak Beraturan: Segi banyak beraturan memiliki semua sisi dan sudut yang sama panjang dan besar. Segi banyak tidak beraturan memiliki sisi dan sudut yang tidak sama.
• Diagonal: Diagonal adalah ruas garis yang menghubungkan dua titik sudut yang tidak berdekatan. Jumlah diagonal pada segi banyak dapat dihitung dengan rumus n(n-3)/2, di mana n adalah jumlah sisi.

Memahami sifat-sifat ini sangat penting dalam menyelesaikan berbagai masalah geometri yang melibatkan segi banyak. Sifat-sifat ini membentuk dasar untuk memahami hubungan antara sisi, sudut, dan luas segi banyak.

Rumus-Rumus Segi Banyak

Berikut adalah beberapa rumus yang berkaitan dengan segi banyak, terutama untuk segi banyak yang umum dipelajari:

• Luas Segitiga: ½ x alas x tinggi. Rumus ini merupakan dasar untuk menghitung luas segitiga, dan dapat dimodifikasi untuk berbagai jenis segitiga.
• Luas Persegi: sisi x sisi. Rumus sederhana ini sangat berguna untuk menghitung luas persegi.
• Luas Persegi Panjang: panjang x lebar. Rumus ini digunakan untuk menghitung luas persegi panjang.
• Luas Jajar Genjang: alas x tinggi. Rumus ini menghitung luas jajar genjang.
• Luas Belah Ketupat: ½ x diagonal 1 x diagonal 2. Rumus ini khusus untuk belah ketupat.
• Luas Trapesium: ½ x (jumlah sisi sejajar) x tinggi. Rumus ini digunakan untuk menghitung luas trapesium.
• Luas Layang-layang: ½ x diagonal 1 x diagonal 2. Rumus ini digunakan untuk menghitung luas layang-layang.

Rumus-rumus ini hanya sebagian kecil dari rumus-rumus yang ada. Rumus yang digunakan tergantung pada jenis segi banyak yang dibahas. Untuk segi banyak dengan jumlah sisi yang lebih banyak, perhitungan luasnya bisa lebih kompleks dan seringkali memerlukan teknik trigonometri atau kalkulus integral. Dalam kasus tersebut, pembagian segi banyak menjadi segitiga-segitiga kecil dapat memudahkan perhitungan.

Perlu diingat bahwa rumus-rumus di atas hanya berlaku untuk segi banyak cembung. Untuk segi banyak cekung, perhitungan luasnya akan lebih kompleks dan memerlukan pendekatan yang berbeda. Terkadang, diperlukan pembagian segi banyak cekung menjadi beberapa segi banyak cembung untuk mempermudah perhitungan.

Aplikasi Segi Banyak dalam Kehidupan Sehari-hari

Segi banyak bukan hanya sekadar konsep matematika abstrak. Konsep segi banyak memiliki banyak sekali aplikasi dalam kehidupan sehari-hari. Berikut beberapa contohnya, yang menunjukkan betapa pentingnya memahami konsep segi banyak:

• Arsitektur dan Desain Bangunan: Banyak bangunan menggunakan bentuk-bentuk segi banyak dalam desainnya, mulai dari rumah-rumah sederhana hingga gedung-gedung pencakar langit yang kompleks. Pemahaman tentang geometri segi banyak sangat penting dalam perencanaan struktur bangunan yang kokoh dan efisien.
• Seni dan Kerajinan: Segi banyak sering digunakan dalam seni dan kerajinan, seperti membuat mosaik, quilting, dan desain grafis. Keterampilan geometri membantu dalam menciptakan karya seni yang indah dan presisi.
• Teknik Sipil: Dalam teknik sipil, pemahaman tentang segi banyak sangat penting dalam perencanaan dan pembangunan infrastruktur seperti jalan raya dan jembatan. Perhitungan yang akurat berdasarkan geometri segi banyak memastikan keamanan dan stabilitas struktur.
• Industri Manufaktur: Banyak produk manufaktur memiliki bentuk segi banyak, sehingga pemahaman tentang geometri segi banyak sangat penting dalam proses desain dan produksi. Desain yang tepat dan presisi bergantung pada pemahaman geometri.
• Pemetaan dan Survei: Dalam pemetaan dan survei, segi banyak digunakan untuk mewakili area-area tertentu pada peta. Akurasi pemetaan bergantung pada pemahaman yang tepat tentang geometri segi banyak.
• Video Games dan Animasi 3D: Model 3D dalam video games dan animasi dibangun dari polygon (segi banyak). Semakin banyak polygon yang digunakan, semakin detail dan realistis model 3D tersebut.
• Kristalografi: Bentuk kristal seringkali memiliki struktur yang berdasarkan pada segi banyak beraturan. Pemahaman tentang geometri segi banyak penting dalam analisis struktur kristal.

Memahami segi banyak sangat penting dalam berbagai bidang, dan pengetahuan ini dapat membantu kita dalam memecahkan masalah dalam kehidupan sehari-hari. Semakin luas aplikasi segi banyak, semakin penting pula pemahaman yang mendalam terhadap konsep ini.

Contoh Soal Segi Banyak

Berikut adalah contoh soal untuk menguji pemahaman Anda tentang segi banyak:

1. Hitunglah jumlah sudut dalam suatu segi delapan!
2. Sebuah segitiga memiliki alas 10 cm dan tinggi 6 cm. Berapakah luas segitiga tersebut?
3. Sebuah persegi panjang memiliki panjang 12 cm dan lebar 8 cm. Berapa keliling dan luas persegi panjang tersebut?
4. Sebuah belah ketupat memiliki diagonal 1 = 16 cm dan diagonal 2 = 12 cm. Berapakah luas belah ketupat tersebut?
5. Sebuah trapesium memiliki sisi sejajar 8 cm dan 12 cm, dan tinggi 5 cm. Berapakah luas trapesium tersebut?
6. Hitunglah jumlah diagonal pada sebuah segi sepuluh!

Cobalah untuk menjawab soal-soal di atas. Jika Anda mengalami kesulitan, Anda dapat meninjau kembali materi yang telah dijelaskan di atas. Mencoba menyelesaikan soal-soal adalah cara terbaik untuk menguji dan memperdalam pemahaman Anda tentang segi banyak.

Selain contoh-contoh di atas, masih banyak lagi aplikasi segi banyak dalam kehidupan nyata. Dari desain pakaian hingga pembangunan jembatan, pemahaman tentang segi banyak sangat diperlukan. Dalam beberapa kasus, pemahaman tentang segi banyak dapat membantu dalam optimisasi desain dan efisiensi material.

Oleh karena itu, mempelajari segi banyak tidak hanya penting untuk memahami konsep matematika dasar, tetapi juga untuk mempersiapkan diri menghadapi tantangan di berbagai bidang profesional. Semakin dalam pemahaman Anda tentang segi banyak, semakin luas pula aplikasi yang dapat Anda terapkan dalam kehidupan sehari-hari. Kemampuan untuk menganalisis dan memecahkan masalah yang berkaitan dengan segi banyak merupakan keterampilan yang sangat berharga.

Ingatlah bahwa kunci utama dalam memahami segi banyak adalah latihan dan pemahaman yang mendalam terhadap konsep-konsep dasarnya. Semakin banyak Anda berlatih mengerjakan soal-soal dan menerapkan konsep-konsep yang telah dipelajari, semakin mahir Anda dalam memahami dan menggunakan pengetahuan tentang segi banyak. Jangan ragu untuk mencari sumber belajar tambahan seperti buku, video tutorial, atau situs web edukatif untuk memperdalam pemahaman Anda.

Kesimpulan

Segi banyak adalah konsep dasar dalam geometri yang memiliki peran penting dalam berbagai bidang. Memahami definisi, jenis, sifat, dan rumus-rumus segi banyak akan membantu Anda dalam memecahkan berbagai masalah dan menerapkannya dalam kehidupan nyata. Semoga artikel ini dapat membantu Anda dalam memahami konsep segi banyak dengan lebih baik dan lebih komprehensif.

Teruslah belajar dan berlatih untuk meningkatkan pemahaman Anda tentang segi banyak. Dengan pemahaman yang mendalam, Anda dapat membuka pintu menuju berbagai peluang dan tantangan di masa depan. Pengetahuan tentang segi banyak akan selalu berguna, baik dalam studi maupun dalam pekerjaan Anda kelak.

Selamat belajar dan semoga artikel ini bermanfaat!