Segi empat, sebuah istilah yang mungkin sudah tidak asing lagi bagi kita sejak bangku sekolah dasar. Bentuk geometris sederhana ini ternyata menyimpan banyak misteri dan keindahan matematika yang menarik untuk dijelajahi. Dari pengertian dasar hingga berbagai jenis dan aplikasinya dalam kehidupan sehari-hari, segi empat hadir dengan kekayaan detail yang sayang untuk dilewatkan. Artikel ini akan membahas secara mendalam tentang segi empat, mulai dari definisi, jenis-jenis, sifat-sifat, hingga penerapannya dalam berbagai bidang.
Secara sederhana, segi empat didefinisikan sebagai bangun datar dua dimensi yang memiliki empat sisi dan empat sudut. Setiap sisi merupakan ruas garis lurus, dan keempat sudutnya merupakan titik pertemuan antara dua sisi yang berdekatan. Definisi ini mungkin tampak sederhana, namun di balik kesederhanaannya tersimpan beragam variasi dan karakteristik yang membedakan satu segi empat dengan segi empat lainnya. Pemahaman yang mendalam tentang segi empat membuka pintu menuju pemahaman yang lebih luas tentang geometri dan aplikasinya dalam berbagai bidang ilmu dan teknologi.
Salah satu hal yang membedakan berbagai jenis segi empat adalah panjang dan sudut antar sisinya. Perbedaan ini melahirkan berbagai jenis segi empat, masing-masing dengan sifat dan rumus perhitungan luas dan keliling yang berbeda pula. Mari kita telusuri lebih jauh berbagai jenis segi empat yang ada. Perjalanan kita akan meliputi berbagai jenis segi empat, mulai dari yang paling sederhana hingga yang lebih kompleks, serta eksplorasi sifat-sifat unik masing-masing.
Jenis-Jenis Segi Empat dan Karakteristiknya
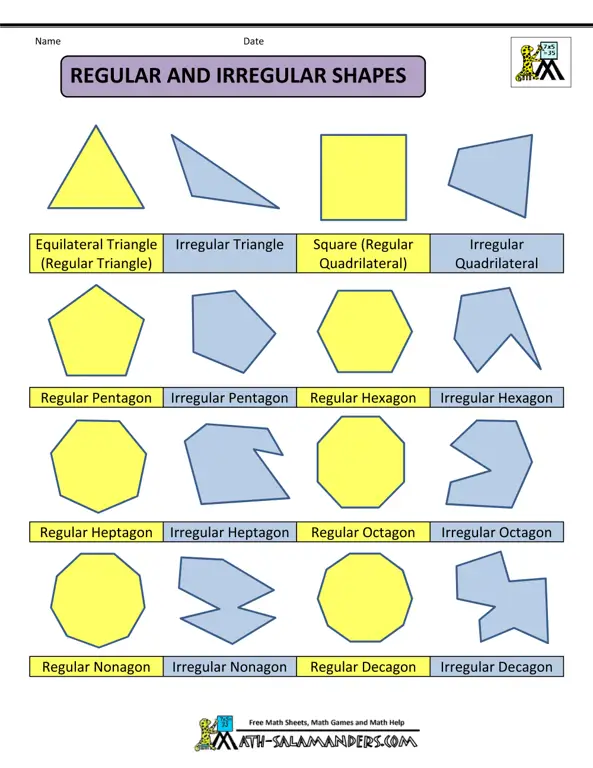
Dunia segi empat sangat beragam. Beberapa jenis segi empat yang paling umum dikenal antara lain:
- Persegi: Segi empat dengan empat sisi yang sama panjang dan empat sudut siku-siku (90 derajat). Persegi merupakan bangun datar yang paling simetris, dengan sifat-sifat yang sangat teratur dan mudah diprediksi.
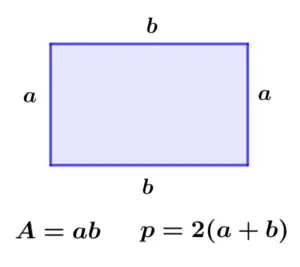
- Persegi Panjang: Segi empat dengan dua pasang sisi yang sama panjang dan empat sudut siku-siku. Persegi panjang sering digunakan dalam berbagai aplikasi karena bentuknya yang praktis dan mudah diukur.
- Belah Ketupat: Segi empat dengan keempat sisi sama panjang, namun sudutnya tidak semuanya siku-siku. Belah ketupat memiliki bentuk yang lebih dinamis dibandingkan persegi dan persegi panjang.
- Jajar Genjang: Segi empat dengan dua pasang sisi yang sejajar dan sama panjang, namun sudutnya tidak semuanya siku-siku. Jajar genjang sering ditemukan dalam berbagai pola dan desain.
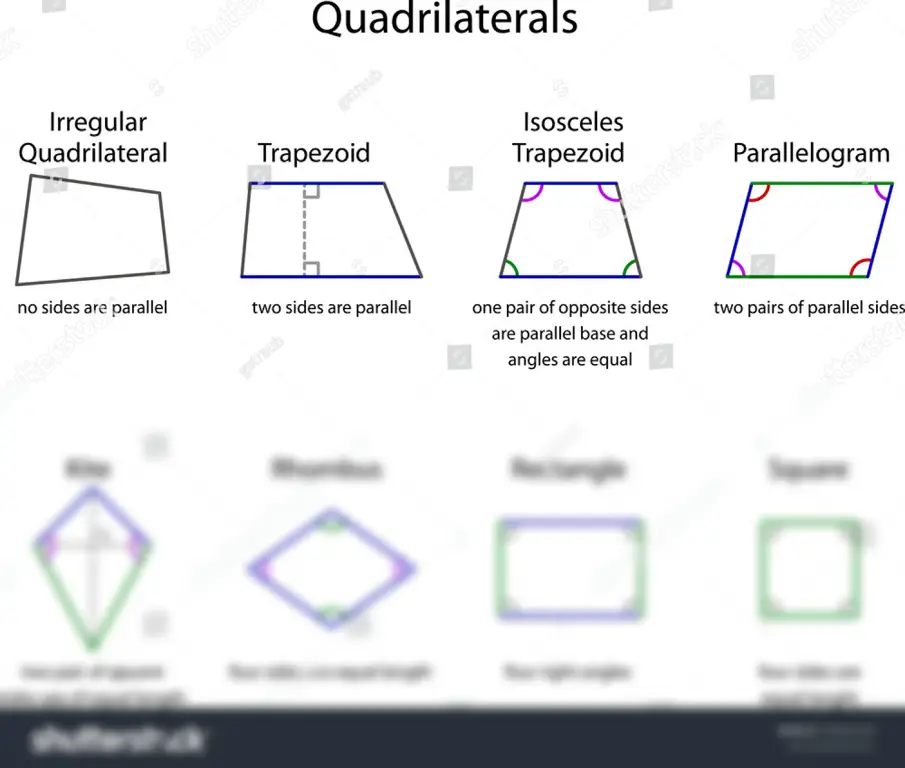
- Trapesium: Segi empat dengan hanya sepasang sisi yang sejajar. Trapesium memiliki bentuk yang lebih variatif dan kurang simetris dibandingkan jenis segi empat lainnya.
- Layang-layang: Segi empat dengan dua pasang sisi yang berdekatan sama panjang. Layang-layang memiliki bentuk yang unik dan sering digunakan dalam berbagai desain.
- Segi Empat Sembarang: Segi empat yang tidak memiliki sifat-sifat khusus dari jenis segi empat lainnya. Ini merupakan kategori yang paling umum dan mencakup berbagai bentuk segi empat yang tidak termasuk dalam kategori di atas. Meskipun tidak memiliki sifat khusus, segi empat sembarang masih mengikuti aturan geometri dasar seperti jumlah sudut dalam yang selalu 360 derajat.
Setiap jenis segi empat memiliki karakteristik unik yang membedakannya. Memahami perbedaan ini sangat penting untuk menyelesaikan berbagai masalah matematika yang berkaitan dengan segi empat, dan juga untuk memahami bagaimana bentuk-bentuk ini diterapkan dalam dunia nyata.
Mari kita bahas lebih detail masing-masing jenis segi empat. Persegi, misalnya, memiliki sifat-sifat unik yang membuatnya mudah dikenali. Keempat sisinya sama panjang dan keempat sudutnya membentuk sudut siku-siku. Luas persegi dihitung dengan rumus sisi x sisi, sementara kelilingnya dihitung dengan rumus 4 x sisi. Sifat-sifat simetris persegi membuatnya sangat cocok untuk berbagai aplikasi, terutama dalam konstruksi dan desain.
Persegi panjang, meskipun memiliki sudut siku-siku seperti persegi, memiliki perbedaan pada panjang sisinya. Ia memiliki dua pasang sisi yang sama panjang, dan luasnya dihitung dengan rumus panjang x lebar. Persegi panjang merupakan bentuk yang sangat umum digunakan dalam berbagai konteks, mulai dari desain bangunan hingga pembuatan kemasan produk.
Belah ketupat, dengan keempat sisinya yang sama panjang, memiliki bentuk yang berbeda dengan persegi. Sudut-sudutnya tidak semuanya siku-siku, melainkan membentuk dua pasang sudut yang sama besar. Rumus luasnya sedikit lebih rumit, melibatkan tinggi dan panjang alas, atau setengah dari hasil kali kedua diagonalnya. Belah ketupat sering ditemukan dalam berbagai motif dan desain, khususnya dalam seni dan kerajinan.
Jajar genjang, mirip dengan belah ketupat, memiliki dua pasang sisi sejajar dan sama panjang. Namun, sudut-sudutnya tidak membentuk sudut siku-siku. Luasnya dihitung dengan rumus alas x tinggi. Jajar genjang memiliki sifat-sifat yang unik yang membuatnya berguna dalam berbagai aplikasi matematika dan fisika.
Trapesium, sebagai segi empat yang hanya memiliki sepasang sisi sejajar, memiliki bentuk yang lebih beragam. Luas trapesium dihitung dengan rumus 1/2 x (jumlah sisi sejajar) x tinggi. Terdapat berbagai jenis trapesium, seperti trapesium siku-siku, trapesium sama kaki, dan trapesium sembarang.
Layang-layang, dengan dua pasang sisi yang berdekatan sama panjang, memiliki bentuk yang khas dan mudah dikenali. Luasnya dihitung dengan rumus 1/2 x diagonal1 x diagonal2. Bentuk layang-layang sering ditemukan dalam berbagai desain dan motif, khususnya dalam karya seni dan kerajinan.
Segi empat sembarang, seperti namanya, tidak memiliki sifat khusus selain memiliki empat sisi dan empat sudut. Luasnya dihitung dengan cara yang lebih kompleks, seringkali melibatkan pembagian menjadi segitiga-segitiga kecil atau penggunaan rumus trigonometri. Meskipun tidak memiliki sifat-sifat yang teratur, segi empat sembarang tetap merupakan bagian penting dari geometri.
Memahami rumus dan sifat-sifat masing-masing jenis segi empat sangat penting dalam memecahkan berbagai soal matematika. Kemampuan untuk mengidentifikasi jenis segi empat dan menerapkan rumus yang tepat akan sangat membantu dalam menyelesaikan masalah geometri, baik dalam konteks akademis maupun dalam aplikasi praktisnya.
Sifat-Sifat Segi Empat dan Hubungannya
Selain jenis-jenisnya, segi empat juga memiliki berbagai sifat geometri yang menarik dan saling berkaitan. Beberapa sifat umum yang dimiliki oleh sebagian besar segi empat antara lain:
- Jumlah sudut dalam segi empat selalu 360 derajat. Ini adalah sifat fundamental yang berlaku untuk semua jenis segi empat, dari yang paling sederhana hingga yang paling kompleks.
- Segi empat memiliki empat sisi dan empat sudut. Ini adalah definisi dasar dari segi empat.
- Diagonal-diagonal segi empat dapat membagi segi empat menjadi beberapa segitiga. Ini merupakan sifat yang berguna untuk menghitung luas segi empat dengan cara yang berbeda.
- Jumlah sudut luar segi empat selalu 360 derajat. Sudut luar dibentuk oleh perpanjangan salah satu sisi segi empat.
Namun, sifat-sifat spesifik akan berbeda-beda tergantung pada jenis segi empatnya. Misalnya, persegi memiliki sifat tambahan seperti keempat sisinya sama panjang dan keempat sudutnya siku-siku. Persegi panjang juga memiliki sudut siku-siku, tetapi sisinya tidak semuanya sama panjang. Belah ketupat memiliki keempat sisinya sama panjang, tetapi sudutnya tidak semuanya siku-siku. Dan seterusnya. Masing-masing jenis segi empat memiliki sifat-sifat unik yang membedakannya dari jenis segi empat lainnya.
Pemahaman mendalam tentang sifat-sifat ini penting untuk membuktikan berbagai teorema geometri dan menyelesaikan masalah-masalah yang lebih kompleks. Dengan memahami sifat-sifat tersebut, kita dapat dengan mudah mengidentifikasi jenis segi empat dan menghitung luas serta kelilingnya dengan tepat. Lebih lanjut, pemahaman ini memungkinkan kita untuk menganalisis dan memecahkan masalah geometri yang lebih rumit.

Hubungan antara berbagai sifat segi empat juga sangat menarik untuk dipelajari. Misalnya, hubungan antara panjang sisi dan besar sudut pada berbagai jenis segi empat. Pada persegi, semua sisi sama panjang dan semua sudut siku-siku. Pada persegi panjang, sisi-sisi yang berhadapan sama panjang dan semua sudut siku-siku. Pada belah ketupat, semua sisi sama panjang, tetapi sudutnya tidak selalu siku-siku. Pada jajar genjang, sisi-sisi yang berhadapan sama panjang dan sejajar, tetapi sudutnya tidak selalu siku-siku. Memahami hubungan-hubungan ini membantu kita untuk lebih memahami karakteristik masing-masing jenis segi empat.
Teorema dan Bukti dalam Geometri Segi Empat
Berbagai teorema dalam geometri berkaitan dengan segi empat. Beberapa teorema yang penting antara lain:
- Teorema Pythagoras: Teorema ini, meskipun tidak secara khusus tentang segi empat, sering digunakan dalam perhitungan yang berkaitan dengan segi empat, khususnya dalam mencari panjang diagonal atau sisi-sisi.
- Teorema tentang jumlah sudut dalam segi empat: Jumlah sudut dalam segi empat selalu 360 derajat. Teorema ini merupakan dasar dari berbagai perhitungan geometri yang berkaitan dengan segi empat.
- Teorema tentang diagonal-diagonal pada berbagai jenis segi empat: Diagonal-diagonal pada persegi dan persegi panjang saling membagi dua sama panjang dan saling tegak lurus. Pada belah ketupat, diagonal-diagonal saling membagi dua sama panjang dan saling tegak lurus. Pada jajar genjang, diagonal-diagonal saling membagi dua sama panjang, tetapi tidak selalu saling tegak lurus.
Membuktikan teorema-teorema ini membutuhkan pemahaman yang mendalam tentang aksioma dan postulat geometri. Bukti-bukti ini biasanya melibatkan penggunaan berbagai metode geometri, seperti penggunaan segitiga kongruen, kesebangunan, dan trigonometri. Dengan memahami bukti-bukti ini, kita dapat lebih memahami dasar-dasar geometri dan bagaimana berbagai konsep geometri saling berkaitan.
Sebagai contoh, bukti teorema jumlah sudut dalam segi empat dapat dilakukan dengan membagi segi empat menjadi dua segitiga. Jumlah sudut dalam setiap segitiga adalah 180 derajat, sehingga jumlah sudut dalam segi empat adalah 180 derajat + 180 derajat = 360 derajat. Ini merupakan contoh sederhana dari bagaimana bukti geometri dapat dilakukan dengan menggunakan konsep-konsep dasar geometri.
Penerapan Segi Empat dalam Berbagai Bidang
Segi empat, meskipun terlihat sederhana, memiliki peran yang signifikan dalam berbagai bidang kehidupan. Kemampuan untuk memahami dan mengaplikasikan konsep segi empat memiliki implikasi yang luas dalam berbagai disiplin ilmu dan teknologi.
Arsitektur dan Teknik Sipil: Bangunan-bangunan, jembatan, dan berbagai struktur lainnya seringkali didesain berdasarkan bentuk segi empat. Persegi dan persegi panjang, misalnya, sangat umum digunakan dalam desain arsitektur untuk menciptakan ruangan-ruangan dengan bentuk yang teratur dan efisien. Pemahaman tentang kekuatan dan stabilitas berbagai jenis segi empat sangat penting dalam perancangan struktur bangunan yang kokoh dan tahan lama.
Desain Grafis dan Seni Rupa: Segi empat digunakan untuk menciptakan komposisi visual yang menarik dan seimbang. Kotak dan persegi panjang sering digunakan sebagai elemen dasar dalam desain logo, poster, dan brosur. Dalam seni rupa, segi empat dapat digunakan untuk menciptakan berbagai efek visual yang menarik. Pemahaman tentang proporsi dan keseimbangan dalam penggunaan segi empat sangat penting dalam menciptakan karya seni yang estetis.
Teknik Mesin dan Manufaktur: Banyak komponen mesin dan produk manufaktur lainnya didesain berdasarkan bentuk segi empat. Ketepatan dan presisi dalam pembuatan komponen-komponen ini sangat penting untuk memastikan kinerja dan keandalan mesin atau produk tersebut. Pemahaman tentang geometri segi empat sangat penting dalam proses desain dan manufaktur ini.
Pemetaan dan Survei: Dalam pemetaan dan survei, segi empat digunakan untuk mewakili berbagai area dan wilayah. Kemampuan untuk menghitung luas dan keliling berbagai jenis segi empat sangat penting dalam pemetaan dan survei.
Ilmu Komputer dan Pemrograman: Konsep segi empat digunakan dalam berbagai algoritma dan program komputer, khususnya dalam bidang grafik komputer dan pengolahan citra. Pemahaman tentang geometri segi empat sangat penting dalam mengembangkan program-program komputer yang efisien dan handal.
Contoh penggunaan segi empat lainnya dapat ditemukan dalam berbagai aspek kehidupan, seperti dalam pembuatan ubin, desain kemasan produk, hingga dalam pembuatan permainan papan. Bentuk segi empat dipilih karena kemudahannya dalam pembuatan, kestabilannya, dan kesederhanaannya dalam memberikan kesan yang rapi dan teratur.
Kesimpulannya, segi empat merupakan bentuk geometris yang sederhana namun sangat penting. Pemahaman yang mendalam tentang jenis-jenis, sifat-sifat, dan rumus-rumusnya tidak hanya penting untuk memahami matematika, tetapi juga memiliki aplikasi yang luas dalam berbagai bidang kehidupan. Dari bangunan megah hingga benda-benda kecil di sekitar kita, segi empat selalu hadir dan memainkan peran penting dalam kehidupan kita sehari-hari.
Lebih dari itu, mempelajari segi empat dapat meningkatkan kemampuan berpikir logis dan analitis. Dengan memahami konsep-konsep geometri dasar seperti ini, kita dapat melatih kemampuan pemecahan masalah dan mengembangkan kecakapan berpikir kritis yang bermanfaat dalam berbagai aspek kehidupan. Segi empat, meskipun tampak sederhana, menyimpan kekayaan pengetahuan dan aplikasi yang tak terbatas. Eksplorasi lebih lanjut tentang segi empat dapat membuka pintu menuju pemahaman yang lebih dalam tentang geometri dan aplikasinya dalam berbagai bidang.

Semoga artikel ini memberikan pemahaman yang lebih komprehensif tentang segi empat. Dengan memahami konsep-konsep dasar ini, kita dapat lebih menghargai keindahan dan kegunaan bentuk geometris yang sederhana namun luar biasa ini. Teruslah belajar dan eksplorasi dunia matematika yang penuh keajaiban!
Berikut adalah tabel ringkasan dari berbagai jenis segi empat beserta sifat-sifat dan rumus luasnya:
| Jenis Segi Empat | Sifat-Sifat | Rumus Luas | Contoh Aplikasi |
|---|---|---|---|
| Persegi | Keempat sisi sama panjang, keempat sudut siku-siku | sisi x sisi | Ubin, papan catur, kotak |
| Persegi Panjang | Dua pasang sisi sama panjang, keempat sudut siku-siku | panjang x lebar | Ruangan, jendela, pintu |
| Belah Ketupat | Keempat sisi sama panjang | 1/2 x diagonal1 x diagonal2 | Layang-layang, motif batik |
| Jajar Genjang | Dua pasang sisi sejajar dan sama panjang | alas x tinggi | Atap rumah, desain grafis |
| Trapesium | Sepasang sisi sejajar | 1/2 x (jumlah sisi sejajar) x tinggi | Potongan lahan, desain konstruksi |
| Layang-layang | Dua pasang sisi yang berdekatan sama panjang | 1/2 x diagonal1 x diagonal2 | Layang-layang mainan, desain logo |
| Segi Empat Sembarang | Tidak memiliki sifat khusus | Rumus yang lebih kompleks (tergantung bentuk) | Bentuk lahan yang tidak beraturan |
Ingatlah bahwa pemahaman yang mendalam tentang segi empat membutuhkan latihan dan penerapan secara konsisten. Cobalah untuk menyelesaikan berbagai soal dan contoh penerapannya dalam kehidupan nyata untuk memperkuat pemahaman Anda. Semakin banyak Anda berlatih, semakin mahir Anda dalam memahami dan mengaplikasikan konsep-konsep geometri yang berkaitan dengan segi empat.