Segi panjang, sebuah istilah yang mungkin sudah familiar bagi kita sejak bangku sekolah dasar. Bentuk geometris yang sederhana namun menyimpan berbagai konsep matematika yang menarik dan mendalam. Dari luas hingga keliling, dari jenis-jenisnya hingga penerapannya dalam kehidupan sehari-hari, segi panjang menyimpan banyak rahasia yang menunggu untuk diungkap. Artikel ini akan membahas secara lengkap dan komprehensif tentang segi panjang, mulai dari definisi dasar hingga aplikasi praktisnya, bahkan membahas konsep-konsep yang lebih kompleks dan jarang dibahas dalam pendidikan dasar. Kita akan menjelajahi dunia segi panjang dengan lebih detail, termasuk bagaimana mengaplikasikan konsep-konsep ini dalam pemecahan masalah sehari-hari dan bahkan dalam konteks yang lebih akademis.
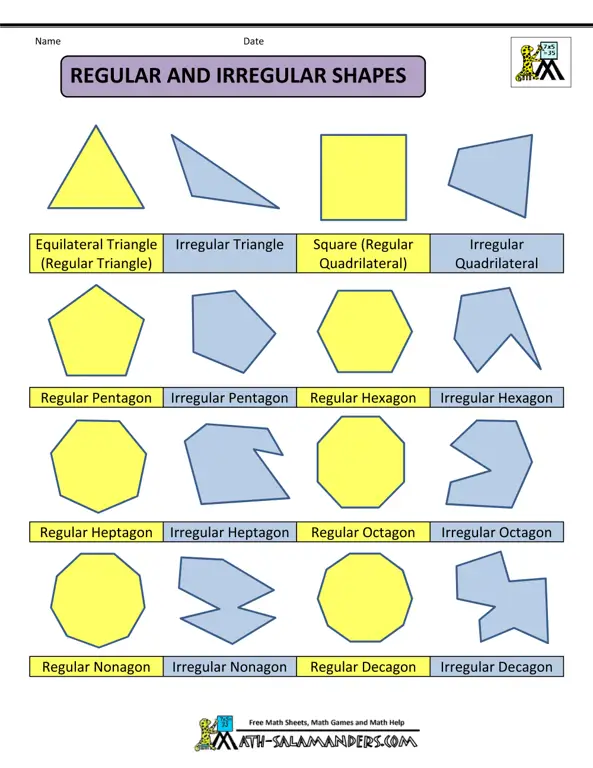
Sebelum kita menyelami lebih dalam, mari kita definisikan terlebih dahulu apa itu segi panjang. Segi panjang, dalam geometri, adalah bangun datar dua dimensi yang memiliki empat sisi dan empat sudut. Keunikan segi panjang terletak pada sifat-sifat khusus yang dimilikinya, yaitu sudut-sudutnya yang semuanya siku-siku (90 derajat) dan sisi-sisinya yang berhadapan sejajar dan sama panjang. Ini merupakan karakteristik utama yang membedakan segi panjang dari bangun datar lainnya. Sifat-sifat ini menjadi kunci dalam memahami berbagai rumus dan aplikasi dari bentuk geometris yang sederhana ini.
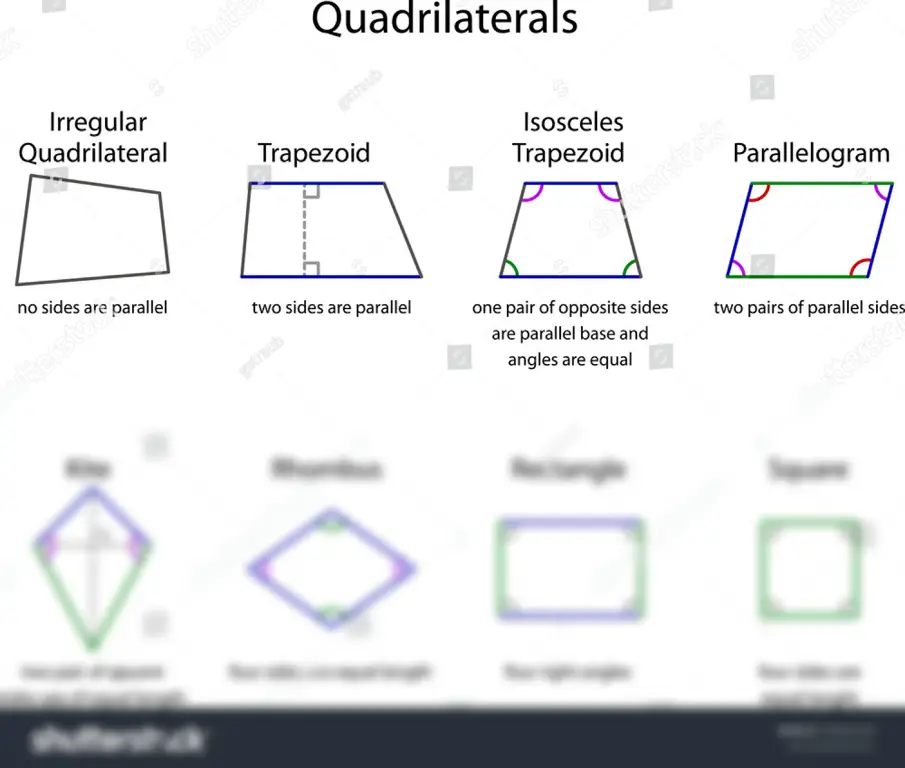
Sifat-sifat inilah yang membedakan segi panjang dari bangun datar lainnya seperti persegi, belah ketupat, atau jajar genjang. Meskipun memiliki kemiripan, terdapat perbedaan mendasar yang membedakannya. Pemahaman yang tepat tentang sifat-sifat segi panjang sangat penting untuk memahami berbagai rumus dan perhitungan yang terkait, serta untuk menyelesaikan berbagai permasalahan geometri yang lebih kompleks. Penguasaan konsep dasar ini akan menjadi pondasi yang kuat untuk mempelajari geometri tingkat lanjut.
Salah satu aspek terpenting dalam mempelajari segi panjang adalah perhitungan luas dan kelilingnya. Rumus luas segi panjang sangat sederhana, yaitu panjang dikali lebar. Rumus ini mudah diingat dan diaplikasikan dalam berbagai konteks, bahkan dalam situasi yang melibatkan perhitungan luas area yang tidak beraturan dengan pendekatan poligon. Dengan memahami rumus dasar ini, kita dapat dengan mudah menghitung luas berbagai objek dalam kehidupan sehari-hari.
Sementara itu, keliling segi panjang dihitung dengan menjumlahkan panjang keempat sisinya, atau bisa juga dihitung dengan rumus 2 x (panjang + lebar). Rumus-rumus ini merupakan dasar dari berbagai perhitungan lanjutan dalam geometri dan trigonometri, sehingga pemahaman yang kuat terhadap rumus dasar ini sangat penting. Penguasaan rumus ini akan membantu kita dalam menyelesaikan berbagai macam masalah geometri yang lebih rumit.
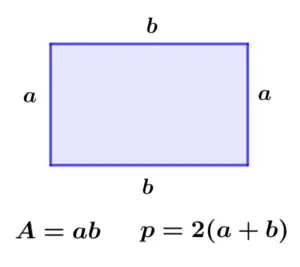
Mari kita ambil contoh sederhana. Misalkan kita memiliki sebuah segi panjang dengan panjang 10 cm dan lebar 5 cm. Luas segi panjang tersebut adalah 10 cm x 5 cm = 50 cm². Sedangkan kelilingnya adalah 2 x (10 cm + 5 cm) = 30 cm. Contoh sederhana ini menggambarkan betapa mudahnya menghitung luas dan keliling segi panjang. Namun, pemahaman ini harus diperluas untuk menghadapi soal-soal yang lebih kompleks dan membutuhkan pemahaman yang lebih mendalam.
Jenis-jenis Segi Panjang dan Sifat-Sifatnya
Meskipun definisi segi panjang tampak sederhana, namun perlu diingat bahwa segi panjang juga memiliki beberapa jenis yang perlu kita ketahui. Perbedaannya terletak pada hubungan antara panjang dan lebarnya. Jenis-jenis segi panjang ini memiliki sifat-sifat unik yang perlu diperhatikan, dan pemahaman ini akan sangat membantu dalam memecahkan masalah geometri yang lebih kompleks. Perbedaan ini seringkali menjadi kunci dalam menyelesaikan masalah geometri yang lebih menantang.
- Persegi Panjang: Merupakan jenis segi panjang yang paling umum. Panjang dan lebarnya berbeda. Ini adalah bentuk segi panjang yang paling sering kita temui dalam kehidupan sehari-hari. Persegi panjang merupakan representasi yang umum dari segi panjang.
- Persegi: Merupakan kasus khusus dari segi panjang dimana panjang dan lebarnya sama. Semua sisinya sama panjang dan semua sudutnya siku-siku. Persegi memiliki sifat simetri yang tinggi dan merupakan contoh khusus dari segi panjang. Persegi seringkali digunakan sebagai contoh ideal dari segi panjang dalam berbagai aplikasi.
Perbedaan antara persegi panjang dan persegi terletak pada kesamaan panjang sisinya. Persegi merupakan kasus khusus dari segi panjang yang memiliki sisi-sisi yang sama panjang. Memahami perbedaan ini sangat penting dalam menyelesaikan berbagai soal geometri, terutama ketika kita berhadapan dengan bangun datar yang lebih kompleks. Perbedaan ini penting untuk diingat agar tidak terjadi kesalahan dalam perhitungan.
Penggunaan rumus luas dan keliling tetap sama untuk kedua jenis segi panjang ini, hanya saja pada persegi, kita dapat menggunakan rumus yang lebih sederhana karena panjang dan lebarnya identik. Untuk persegi, luasnya adalah sisi x sisi, dan kelilingnya adalah 4 x sisi. Kesederhanaan rumus ini tidak mengurangi pentingnya pemahaman konsep di baliknya. Pemahaman yang mendalam tentang konsep ini akan sangat membantu dalam berbagai aplikasi.
Menghitung Luas dan Keliling Segi Panjang dalam Konteks yang Lebih Kompleks
Perhitungan luas dan keliling segi panjang menjadi lebih kompleks ketika kita berhadapan dengan situasi yang melibatkan bangun datar yang tidak beraturan. Dalam kasus seperti ini, kita perlu membagi bangun datar tersebut menjadi beberapa segi panjang yang lebih sederhana, kemudian menghitung luas masing-masing bagian dan menjumlahkannya untuk mendapatkan luas total. Ini merupakan aplikasi penting dari pemahaman dasar tentang segi panjang. Kemampuan untuk memecah masalah kompleks menjadi bagian-bagian yang lebih sederhana merupakan keterampilan yang sangat berharga.
Sebagai contoh, bayangkan sebuah lahan pertanian yang berbentuk huruf L. Lahan ini dapat dibagi menjadi dua buah segi panjang. Dengan menghitung luas masing-masing segi panjang, kita dapat menghitung luas total lahan tersebut. Begitu pula dengan kelilingnya, kita perlu menghitung keliling masing-masing segi panjang dan menjumlahkannya, dengan memperhatikan bagian yang berhimpitan. Ini membutuhkan pemahaman yang lebih mendalam tentang geometri dan kemampuan untuk memecah masalah kompleks menjadi bagian-bagian yang lebih sederhana. Pemahaman ini sangat penting dalam berbagai aplikasi praktis.
Contoh lain adalah perhitungan luas dinding yang tidak beraturan. Kita bisa membagi dinding tersebut menjadi beberapa segi panjang, kemudian menghitung luas masing-masing bagian dan menjumlahkannya. Ini sangat berguna dalam perencanaan pembangunan, desain interior, dan berbagai aplikasi praktis lainnya. Kemampuan untuk memecah masalah kompleks dan menerapkan prinsip-prinsip dasar geometri sangat penting dalam berbagai bidang kehidupan. Ini menunjukkan pentingnya pemahaman konsep geometri dalam kehidupan sehari-hari.
Penerapan Segi Panjang dalam Kehidupan Sehari-hari
Segi panjang bukanlah sekadar konsep matematika abstrak. Bentuk geometris ini memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Kita dapat menemukannya di berbagai tempat, mulai dari bangunan hingga benda-benda di sekitar kita. Penggunaan segi panjang dalam kehidupan sehari-hari begitu luas dan seringkali tidak disadari. Memahami aplikasinya akan meningkatkan apresiasi kita terhadap konsep ini.
Contoh paling sederhana adalah ruangan di dalam rumah kita. Kebanyakan ruangan dirancang dengan bentuk segi panjang untuk memaksimalkan ruang dan efisiensi penggunaan. Begitu pula dengan lahan pertanian, banyak lahan pertanian yang berbentuk segi panjang untuk memudahkan pengelolaan dan penanaman. Efisiensi dan kemudahan penggunaan merupakan alasan utama di balik penggunaan bentuk segi panjang ini. Ini menunjukkan pentingnya segi panjang dalam desain dan perencanaan.
Selain itu, segi panjang juga digunakan dalam desain berbagai produk, seperti buku, kertas, layar monitor, kartu kredit, perangko, dan masih banyak lagi. Bentuk segi panjang dipilih karena kepraktisannya, kemudahan produksinya, dan efisiensi penggunaan ruang. Kita seringkali tidak menyadari betapa banyak objek di sekitar kita yang didesain berdasarkan prinsip segi panjang. Ini menunjukkan betapa luasnya aplikasi segi panjang dalam berbagai produk.
Bahkan dalam bidang konstruksi, segi panjang menjadi dasar perhitungan dalam membangun struktur bangunan. Arsitek dan insinyur menggunakan prinsip-prinsip geometri, termasuk segi panjang, untuk merancang bangunan yang kokoh dan fungsional. Perhitungan luas dan volume seringkali melibatkan perhitungan yang berbasis pada bangun segi panjang. Ini menunjukkan pentingnya pemahaman konsep segi panjang dalam bidang teknik dan arsitektur. Konsep ini menjadi pondasi dalam perencanaan dan pembangunan.
Segi Panjang dalam Bidang Seni dan Desain
Penggunaan segi panjang tidak hanya terbatas pada bidang sains dan teknologi. Dalam seni dan desain, segi panjang juga memainkan peran penting. Banyak karya seni dan desain grafis yang menggunakan segi panjang sebagai elemen dasar komposisinya. Penggunaan segi panjang dapat menciptakan kesan yang berbeda-beda, mulai dari kesan formal hingga kesan dinamis, tergantung pada bagaimana segi panjang tersebut digunakan dalam komposisi. Segi panjang memberikan fleksibilitas dalam desain.
Misalnya, dalam desain web, tata letak yang berbasis pada grid segi panjang dapat menciptakan tampilan yang rapi dan terstruktur. Dalam desain grafis, segi panjang dapat digunakan untuk menciptakan efek visual yang menarik dan membingkai elemen-elemen penting dalam sebuah karya seni. Penggunaan segi panjang dalam seni dan desain menunjukkan sisi estetika dan fungsionalitas yang dimiliki oleh bentuk geometris sederhana ini. Segi panjang memberikan keseimbangan estetika dan fungsionalitas.
Segi Panjang dan Geometri Lanjutan
Konsep segi panjang merupakan dasar bagi pemahaman berbagai konsep geometri yang lebih kompleks. Sebagai contoh, konsep luas dan keliling segi panjang menjadi landasan bagi perhitungan luas dan keliling bangun datar yang lebih kompleks, seperti trapesium, layang-layang, dan sebagainya. Pemahaman yang kuat tentang segi panjang sangat penting sebagai pondasi bagi pembelajaran geometri tingkat lanjut. Segi panjang adalah kunci untuk memahami geometri yang lebih kompleks.
Selain itu, konsep segi panjang juga berkaitan erat dengan konsep trigonometri. Dalam trigonometri, segi panjang sering digunakan sebagai alat bantu untuk memahami dan menyelesaikan berbagai permasalahan trigonometri. Pemahaman tentang segi panjang menjadi kunci bagi pemahaman yang lebih dalam tentang konsep trigonometri. Konsep ini menjadi jembatan menuju pemahaman trigonometri yang lebih baik.
Menghitung Luas dan Keliling Segi Panjang yang Kompleks: Strategi dan Teknik
Seperti yang telah dibahas sebelumnya, menghitung luas dan keliling segi panjang menjadi lebih kompleks ketika kita berhadapan dengan bangun datar yang tidak beraturan atau terdiri dari beberapa segi panjang yang saling berkaitan. Dalam kasus seperti ini, diperlukan strategi dan teknik khusus untuk menyelesaikan perhitungan dengan akurat. Pemahaman yang mendalam diperlukan untuk menyelesaikan perhitungan yang lebih kompleks.
Salah satu strategi yang efektif adalah dengan membagi bangun datar kompleks tersebut menjadi beberapa segi panjang yang lebih sederhana. Kemudian, kita dapat menghitung luas atau keliling masing-masing bagian dan menjumlahkannya untuk mendapatkan hasil total. Ini memerlukan pemahaman yang baik tentang geometri dan kemampuan untuk mengidentifikasi bentuk-bentuk geometris dasar dalam bangun datar yang lebih kompleks. Kemampuan untuk memecah masalah merupakan keterampilan yang sangat penting.
Selain itu, penggunaan rumus dan teorema geometri yang relevan juga sangat penting dalam menyelesaikan perhitungan luas dan keliling segi panjang yang kompleks. Pemahaman yang mendalam tentang konsep geometri dasar akan sangat membantu dalam menyelesaikan permasalahan yang lebih menantang. Penggunaan rumus dan teorema yang tepat sangat krusial.
| Panjang | Lebar | Luas | Keliling |
|---|---|---|---|
| 10 cm | 5 cm | 50 cm² | 30 cm |
| 15 cm | 8 cm | 120 cm² | 46 cm |
| 20 cm | 12 cm | 240 cm² | 64 cm |
| 25 cm | 15 cm | 375 cm² | 80 cm |
| 30 cm | 18 cm | 540 cm² | 96 cm |
Tabel di atas menunjukkan contoh perhitungan luas dan keliling untuk beberapa segi panjang dengan ukuran yang berbeda. Dengan memahami konsep dasar dan rumus-rumus yang terkait, kita dapat dengan mudah menghitung luas dan keliling segi panjang, baik yang sederhana maupun yang kompleks. Latihan dan pemahaman yang mendalam sangat penting untuk menguasai konsep ini. Praktik dan latihan akan meningkatkan pemahaman dan kemampuan.
Segi panjang juga memiliki hubungan erat dengan konsep fraksi dan desimal. Bayangkan sebuah segi panjang yang dibagi menjadi beberapa bagian yang sama. Kita dapat menggunakan konsep fraksi untuk mewakili bagian-bagian tersebut. Begitu pula dengan desimal, kita dapat menggunakan desimal untuk mewakili bagian-bagian dari segi panjang tersebut. Ini menunjukkan keterkaitan segi panjang dengan konsep matematika lainnya.
Lebih lanjut, segi panjang dapat digunakan untuk menjelaskan konsep skala dan perbandingan. Bayangkan sebuah peta yang menunjukkan sebuah lahan berbentuk segi panjang. Kita dapat menggunakan skala untuk mengetahui ukuran sebenarnya dari lahan tersebut. Konsep ini penting dalam kartografi dan berbagai bidang lainnya. Segi panjang membantu kita memahami konsep skala dan perbandingan.
Dalam konteks kalkulus, segi panjang dapat digunakan sebagai dasar untuk menghitung luas daerah di bawah kurva. Konsep ini sangat penting dalam kalkulus integral. Kita dapat mendekati luas daerah tersebut dengan menggunakan sejumlah besar segi panjang kecil. Konsep ini menunjukkan peran segi panjang dalam kalkulus.
Konsep segi panjang juga dapat diperluas ke dalam geometri tiga dimensi, seperti kuboid. Kuboid adalah bangun ruang yang dibatasi oleh enam sisi segi panjang. Kita dapat menggunakan konsep segi panjang untuk menghitung volume kuboid. Ini menunjukkan keterkaitan segi panjang dengan bangun ruang.
Dalam kesimpulannya, segi panjang merupakan bangun datar yang sederhana namun memiliki peran penting dalam matematika dan kehidupan sehari-hari. Memahami sifat-sifat, rumus, dan penerapannya sangatlah penting, tidak hanya untuk akademis, tetapi juga untuk memecahkan masalah praktis dalam berbagai bidang. Semoga artikel ini memberikan pemahaman yang lebih mendalam tentang segi panjang dan aplikasinya dalam berbagai konteks yang lebih kompleks. Segi panjang merupakan konsep dasar yang penting dalam matematika dan kehidupan sehari-hari.